钟昱丰的博客

@TOC
接上文LeetCode算法题解——二分查找2，本篇分享LeetCode中几道比较难想到使用二分查找解法的题目。

第八题

540. 有序数组中的单一元素

题目描述：
给你一个仅由整数组成的有序数组，其中每个元素都会出现两次，唯有一个数只会出现一次。

请你找出并返回只出现一次的那个数。

你设计的解决方案必须满足 O(log n) 时间复杂度和 O(1) 空间复杂度。

示例1：

输入: nums = [1,1,2,3,3,4,4,8,8]
输出: 2

思路

我们先思考一下，没有单一元素的nums，如[1,1,3,3,4,4,8,8]具有什么样的规律。不难发现，对于每一个偶数下标i=2k的nums[i]，它的值都等于后一位nums[i+1]的值。但是在插入2之后，这种规律只会在2之前存在。在2之后，所有奇数下标i=2k+1的nums[i]，都等于nums[i+1]。

所以，我们只需要找到中点m附近的偶数下标，通过判断nums[i]=nums[i+1]这种规律是否存在，就可以判断中点m是在插入的单一元素之前还是之后。如果这种规律存在，那么说明中点m在单一元素之前，需要收缩左边界；如果这种规律不存在，那么说明中点m在单一元素之后，需要收缩右边界。

收缩左边界时，因为已经知道nums[m] = nums[m+1]，所以l=m+2。收缩右边界时，nums[m] != nums[m+1]，则必定有nums[m+1]= nums[m+2]，所以r=m。

最后，搜索区间不断缩小，不断将成对的元素排除在区间之外。当区间长度为1时，区间内的元素就是单一元素。

代码

java版本

class Solution {
    public int singleNonDuplicate(int[] nums) {
        int l = 0, h = nums.length - 1;
        while (l < h) {
        	// 防止溢出
            int m = l + (h - l) / 2;
            if (m % 2 == 1) {
                m--;   // 保证 l/h/m 都在偶数位，使得查找区间大小一直都是奇数
            }
            if (nums[m] == nums[m + 1]) {
                l = m + 2;
            } else {
                h = m;
            }
        }
        return nums[l];
    }
}

python版本

class Solution:
    def singleNonDuplicate(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        while l < r:
            m = l + (r - l) // 2
            if m % 2 == 1:
                m -= 1
            
            if nums[m] == nums[m + 1]:
                l = m + 2
            else:
                r = m
        return nums[l]

总结

之前的二分查找是查找一个target，这道题的二分查找是查找一种关系。某个点之前，这种关系满足，在某个点之后，这种关系不满足。我们需要通过判断关系的满足与否，缩小搜索区间，找出这个点。

第九题

153. 寻找旋转排序数组中的最小值

题目描述：
已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例1:

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

思路

根据单调性，对于升序nums，其任意一点m，其右侧任意一点都大于等于左侧任意一点，即nums[m+] >= nums[m-]。如果发生旋转，则在旋转点k，其右侧任意一点都小于等于左侧任意一点，即nums[k+] <= nums[k-]。通过上一题，我们可以知道，二分查找可以通过缩小搜索区间，找出这种使关系发生变化的点。

旋转点左侧为第一分枝，右侧为第二分枝。我们的目标就是，通过缩小收缩区间，找到第二分枝的左端点，即为旋转点。如果中点m在第二分枝上，根据单调性，有r > m && nums[r] >= nums[m]，那么收缩r=m，使得r保持在第二分枝上。如果r=m-1的话，无法保证还在第二分枝，因为我们只验证过r和m的单调性，没有验证r和m-1的单调性。如果中点m在第一分枝上，则恰好r在旋转点（即第二分枝左端点）右侧，m在旋转点左侧，有nums[r] < nums[m]，那么抛弃中点m及其左边的点，l=m+1。

代码

java版本

class Solution {
    public int findMin(int[] nums) {
        int l = 0, h = nums.length - 1;
        while (l < h) {
            int m = l + (h - l) / 2;
            if (nums[m] <= nums[h]) {
                h = m;
            } else {
                l = m + 1;
            }
        }
        return nums[l];
    }
}

python版本

class Solution:
    def findMin(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if nums[m] == nums[r]:
                break
            elif nums[r] < nums[m]:
                l = m + 1
            else:
                r = m 
        return nums[l]

总结

上面两道题使用二分查找解题的关键都在于，能够将要找的target与某种关系联系起来。在target的左侧，满足某种关系；在target的右侧，不满足这种关系。

第十题

154. 寻找旋转排序数组中的最小值 II

代码

python版本

class Solution:
    def findMin(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if nums[r] == nums[m]:
                r -= 1
            elif nums[r] > nums[m]:
                r = m
            else:
                l = m + 1
        return nums[l]

第十一题

240. 搜索二维矩阵 II

题目描述：
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例1：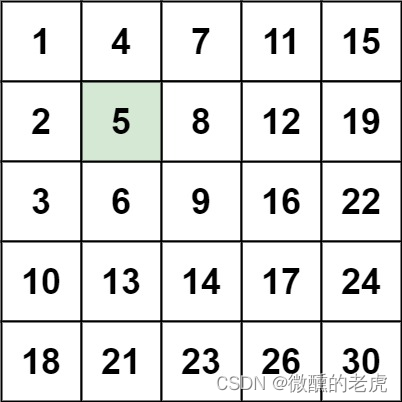

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

思路

在上面两道题中我已经谈到了，可以使用二分查找将target与某种关系联系起来，在target的左侧满足某种关系，而在target的右侧不满足这种关系。在这道题中，这种关系是结构上的。对于任意一个元素，其所在行自左向右递增，所在列自上而下递增。特别的，对于每一行最右的元素m，其左的所在行元素都比它小，其下的所在列元素都比它大。因此，如果给定一个target和m进行比较，target小于m则应该向其左的所在行元素继续比较；target大于m则应该向其下的所在列元素继续比较。如果m的位置超出矩阵的合法范围，则说明找不到target。

代码

java版本

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int i = 0, j = n - 1;
        while(i < m && j >= 0){
            if(target == matrix[i][j]){
                return true;
            }
            else if(target < matrix[i][j]){
                j--;
                continue;
            }
            else{
                i++;
            }
        }
        return false;     
    }
}

python版本

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m = len(matrix)
        n = len(matrix[0])
        x, y = 0, n - 1
        while x < m and y >= 0:
            if matrix[x][y] == target:
                return True
            elif matrix[x][y] < target:
                x += 1
            else:
                y -= 1
                
        return False

总结

这一题和前面两题一样，都需要寻找一种关系作为突破口。在某个点之前，这种关系存在；在某个点之后，这种关系不存在。

第十二题

378. 有序矩阵中第 K 小的元素

题目描述：
给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是 排序后 的第 k 小元素，而不是第 k 个 不同 的元素。

你必须找到一个内存复杂度优于 O(n2) 的解决方案。

示例1：

输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13

思路

我们先分析这道题为什么可以用二分查找来解决。正如前面三题所示，能够用二分查找解决的问题都存在一种关系，在target之前满足这种关系，在target之后不满足这种关系。让我们来看示例1，在数组[1,5,9,10,11,12,13,13,15]中，如果一个元素是target，那么数组中比它小的元素有8个；如果一个元素小于target，那么数组中比它小的元素小于8个；如果一个元素大于target，那么数组中比它小的元素大于8个。这种关系的存在，使得我们可以用二分查找来解决这道题。在这里，给出一个二分查找的思路作为参考，二分，超级简单。

关于这个思路，很多人会纠结的一点是，如何验证最后求得的l在数组中？其实就是在问，如果一个元素是target，那么数组中比它小的元素有8个；反过来，如果数组中比一个数小的元素有8个，那么这个元素到底是不是target？不难发现，“一个元素是target，那么数组中比它小的元素有8个”是个充分不必要条件。不妨把数组[1,5,9,10,11,12,13,13,15]最后的15改成30来讨论这个问题。对于数组[1,5,9,10,11,12,13,13,30]，我们还是寻找第8小的元素，正确答案应该是13。但是，在13和30中间，其实还有很多个数满足“数组中比一个数小的元素有8个”这个条件。准确来说，14，15，…，29都满足这个条件。我称这些数为“影子target”。很多人就会纠结，按照二分，超级简单的思路，那么如何排除掉这些“影子target”？这里我们就得先想明白，为什么会存在“影子target”。简单来说，“影子target”就是target和target后一位之间的间隙。如果我们把最后一位改成20，那么正确答案还是13，“影子target”是14，15，…，19。如果我们把数组改成[1,5,9,10,11,12,13,16,20]，那么正确答案是16，“影子target”是17，18，19。那么，我们会发现，16是满足“数组中比一个数小的元素有8个”这个条件的最小的数。

让我们从头思考一下这个问题。为什么我们可以用二分查找来解决这道问题？因为在数组中，如果一个元素是target，那么数组中比它小的元素个数cnt等于8；如果一个元素小于target，那么数组中比它小的元素个数cnt小于8；如果一个元素大于target，那么数组中比它小的元素cnt大于8。所以，我们可以用二分查找解决这道题。cnt小于8，则l=m+1；cnt大于8，则r=m-1。但是，cnt等于8时，我们就找到target了吗？上面已经分析过了，如果cnt等于8，那么这个元素不一定是target，还有可能是“影子target”。因为在target和target后一位之间，还有间隙。那么我们如何找到正确的target呢？我们已经发现，真实target就是满足cnt等于8的最小值，所以我们就是在找满足cnt等于8这个条件的左边界。既然是找左边界，在上一篇博客中我已经讨论过了，其实就是在找到满足cnt等于8这个条件的元素时，不要直接返回结果，而是继续收缩右边界。

代码

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        int n = matrix.length, l = matrix[0][0], r = matrix[n - 1][n - 1], cnt = 0;
        while(l <= r){
            int m = l + (r - l) / 2;
            cnt = 0;
            for(int i = 0; i < n; i++){
                for(int j = 0; j < n && matrix[i][j] <= m; j++){
                    cnt++;
                }
            }
            if(cnt < k){
                l = m + 1;
            }
            else{
                r = m - 1;
            }
        }
        return l;
    }
}

python版本

class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        n = len(matrix)
        l = matrix[0][0]
        r = matrix[n - 1][n - 1]
        while l <= r:
            m = l + (r - l) // 2
            count = 0
            for row in matrix:
                for col in row:
                    if col <= m:
                        count += 1
            
            if k > count:
                l = m + 1
            else:
                r = m - 1

        return l

总结

这道题不难想到用二分查找来解决。一般人或许可以想到用官方题解差不多的二分法。但是，上面介绍的二分法，需要对为什么可以用二分法，用二分法是查找target还是左/右边界有深刻的理解。

参考：
Leetcode 题解 - 二分查找
二分，超级简单