钟昱丰的博客
0%

发表于 分类于
本文字数： 1.7k 阅读时长 ≈ 3 分钟

初始化

在c++中，vector是一个类模板，当使用模板的时候，我们需要指出编译器应该把类和函数实例化成何种类型。

1
2
vector<int> ivec;//vector的元素是int型数据
vector<vector<string>> file;//vector的元素还是是vector对象，这个vector对象的元素是string型数据
阅读全文 »

发表于 分类于
本文字数： 194 阅读时长 ≈ 1 分钟

最近出了高考成绩，有些学弟学妹找我咨询志愿填报的问题。
无论是“地域优先论”，还是“学校优先论”，或者是“专业优先论”，我都持平等的看法。
读大学，说到底还是对一个人基本素质的培养，其他都是虚的。不过，为了满足学弟学妹们的需要，我也整理了一些资料，提供给大家。

阅读全文 »

发表于 分类于
本文字数： 294 阅读时长 ≈ 1 分钟

当你在GitHub中当仓库设置为private时，对外是不可见的，对方无法从GitHub主页查找你，也无法通过你分享的网址查找你。
想要让其他人加入到这个私人项目中，可以添加合作者。

阅读全文 »

发表于
本文字数： 2.8k 阅读时长 ≈ 5 分钟

@TOC

第一题

707. 设计链表 - 力扣（LeetCode）

代码

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class MyLinkedList:

    def __init__(self):
        self.dummy = ListNode(-1)
        self.size = 0

    def get(self, index: int) -> int:
        if index < 0 or index >= self.size:
            return -1

        cur = self.dummy.next
        i = 0
        while i < index:
            cur = cur.next
            i += 1

        return cur.val

    def addAtHead(self, val: int) -> None:
        self.addAtIndex(0, val)

    def addAtTail(self, val: int) -> None:
        self.addAtIndex(self.size, val)

    def addAtIndex(self, index: int, val: int) -> None:
        if index < 0:
            index = 0
        elif index > self.size:
            return

        pre = self.dummy
        i = 0
        while i < index:
            pre = pre.next
            i += 1

        pre.next = ListNode(val, pre.next)
        self.size += 1
        return

    def deleteAtIndex(self, index: int) -> None:
        if index < 0 or index >= self.size:
            return

        pre = self.dummy
        i = 0
        while i < index:
            pre = pre.next
            i += 1

        pre.next = pre.next.next
        self.size -= 1
        return

第二题

876. 链表的中间结点 - 力扣（LeetCode）

代码

python版本

1
2
3
4
5
6
7
8
class Solution:
    def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        slow = fast = head
        while fast and fast.next:
            fast = fast.next.next
            slow = slow.next

        return slow

第三题

203. 移除链表元素 - 力扣（LeetCode）

代码

python版本

1
2
3
4
5
6
7
8
9
10
class Solution:
    def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
        dummy = ListNode(-1, head)
        cur = dummy
        while cur.next:
            if cur.next.val == val:
                cur.next = cur.next.next
            else:
                cur = cur.next
        return dummy.next

第四题

83. 删除排序链表中的重复元素 - 力扣（LeetCode）

代码

python版本

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:
        dummy = ListNode(-101, head)
        cur = dummy
        while cur.next:
            if cur.val == cur.next.val:
                cur.next = cur.next.next
            else:
                cur = cur.next
        
        return dummy.next

第五题

19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

代码

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
        dummy = ListNode(-1, head)
        slow = fast = dummy

        i = 0
        while i < n:
            fast = fast.next
            i += 1

        while fast.next:
            fast = fast.next
            slow = slow.next

        slow.next = slow.next.next
        return dummy.next

发表于
本文字数： 4k 阅读时长 ≈ 7 分钟

@TOC

这里介绍双指针在数组中的第二类题型：两端夹击。

第五题

977. 有序数组的平方

题目描述：
给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例1:

1
2
3
4
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

思路

因为是排序每个数字的平方，根据二次函数图像y=x^2开口向上可得，最大值在两端，最小值在中间。所以，最左和最右进行比较，两端夹击，看谁的平方值更大。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int[] sortedSquares(int[] nums) {
        int n = nums.length;
        int[] result = new int[n];
        int l = 0;
        int r = n - 1;
        int k = n - 1;
        while(l <= r){
            if(nums[l] * nums[l] > nums[r] * nums[r]){
                result[k] = nums[l] * nums[l];
                l++;
                k--;
            }
            else{
                result[k] = nums[r] * nums[r];
                r--;
                k--;
            }
        }
        return result;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        n = len(nums)
        result = [0] * n
        l, r, idx = 0, n - 1, n - 1
        while l <= r:
            numl = nums[l] * nums[l]
            numr = nums[r] * nums[r]
            if numl > numr:
                result[idx] = numl
                idx -= 1
                l += 1
            else:
                result[idx] = numr
                idx -= 1
                r -= 1

        return result

第六题

167. 两数之和 II - 输入有序数组

题目描述:
给定一个已按照升序排列的有序数组，找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

示例1:

1
2
3
输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

思路

可以先考虑边界情况。升序数组中任意两个元素求和，最小为nums[0]+nums[1]，最大为nums[n-2]+nums[n-1]。target的范围一定在这两者之间，否则找不到答案。所以，我们可以两端夹击，一直手抓nums[0]，另一只手抓nums[n-1]。如果是最小的情况，那么让nums[n-1]向nums[1]靠拢；如果是最大的情况，那么让nums[1]向nums[n-2]靠拢。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int l = 0, r = numbers.length - 1;
        int[] result = new int[]{0, 0};
        while(l < r){
            int sum = numbers[l] + numbers[r];
            if(sum == target){
                result[0] = l + 1;
                result[1] = r + 1;
                break;
            }
            else if(sum < target){
                l++;
            }
            else{
                r--;
            }
        }
        return result;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        n = len(numbers)
        l, r = 0, n - 1
        while l < r:
            m = numbers[l] + numbers[r]
            if m == target:
                return [l + 1, r + 1]
            elif target > m:
                l += 1
            else:
                r -= 1
        
        return [-1, -1]

第七题

633. 平方数之和

题目描述:
给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得 a^2 + b^2 = c 。

示例1:

1
2
3
输入：c = 5
输出：true
解释：1 * 1 + 2 * 2 = 5

思路

上一题是两个数的和是否为target，这道题是两个数的平方和是否为target。一样的思路，考虑最大最小值。若两个数的平方和为target，则最小为0，最大为target的平方根。同样的，两端夹击。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean judgeSquareSum(int c) {
        long l = 0;
        long r = (long) Math.sqrt(c);
        while(l <= r){
            long m = l * l + r * r;
            if(m == c){
                return true;
            }
            else if(m < c){
                l++;
            }
            else{
                r--;
            }
        }
        return false;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def judgeSquareSum(self, c: int) -> bool:
        l, r = 0, int(sqrt(c))
        while l <= r:
            m = l * l + r * r
            if m == c:
                return True
            elif m < c:
                l += 1
            else:
                r -= 1
        
        return False

下一篇博客LeetCode算法题解——双指针3中，我将分享LeetCode中关于字符串的双指针问题。

参考：

Leetcode 题解 - 双指针

发表于
本文字数： 8.2k 阅读时长 ≈ 15 分钟

@TOC
接上文LeetCode算法题解——二分查找2，本篇分享LeetCode中几道比较难想到使用二分查找解法的题目。

第八题

540. 有序数组中的单一元素

题目描述：
给你一个仅由整数组成的有序数组，其中每个元素都会出现两次，唯有一个数只会出现一次。

请你找出并返回只出现一次的那个数。

你设计的解决方案必须满足 O(log n) 时间复杂度和 O(1) 空间复杂度。

示例1：

1
2
输入: nums = [1,1,2,3,3,4,4,8,8]
输出: 2

思路

我们先思考一下，没有单一元素的nums，如[1,1,3,3,4,4,8,8]具有什么样的规律。不难发现，对于每一个偶数下标i=2k的nums[i]，它的值都等于后一位nums[i+1]的值。但是在插入2之后，这种规律只会在2之前存在。在2之后，所有奇数下标i=2k+1的nums[i]，都等于nums[i+1]。

所以，我们只需要找到中点m附近的偶数下标，通过判断nums[i]=nums[i+1]这种规律是否存在，就可以判断中点m是在插入的单一元素之前还是之后。如果这种规律存在，那么说明中点m在单一元素之前，需要收缩左边界；如果这种规律不存在，那么说明中点m在单一元素之后，需要收缩右边界。

收缩左边界时，因为已经知道nums[m] = nums[m+1]，所以l=m+2。收缩右边界时，nums[m] != nums[m+1]，则必定有nums[m+1]= nums[m+2]，所以r=m。

最后，搜索区间不断缩小，不断将成对的元素排除在区间之外。当区间长度为1时，区间内的元素就是单一元素。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int singleNonDuplicate(int[] nums) {
        int l = 0, h = nums.length - 1;
        while (l < h) {
        	// 防止溢出
            int m = l + (h - l) / 2;
            if (m % 2 == 1) {
                m--;   // 保证 l/h/m 都在偶数位，使得查找区间大小一直都是奇数
            }
            if (nums[m] == nums[m + 1]) {
                l = m + 2;
            } else {
                h = m;
            }
        }
        return nums[l];
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def singleNonDuplicate(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        while l < r:
            m = l + (r - l) // 2
            if m % 2 == 1:
                m -= 1
            
            if nums[m] == nums[m + 1]:
                l = m + 2
            else:
                r = m
        return nums[l]

总结

之前的二分查找是查找一个target，这道题的二分查找是查找一种关系。某个点之前，这种关系满足，在某个点之后，这种关系不满足。我们需要通过判断关系的满足与否，缩小搜索区间，找出这个点。

第九题

153. 寻找旋转排序数组中的最小值

题目描述：
已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例1:

1
2
3
输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

思路

根据单调性，对于升序nums，其任意一点m，其右侧任意一点都大于等于左侧任意一点，即nums[m+] >= nums[m-]。如果发生旋转，则在旋转点k，其右侧任意一点都小于等于左侧任意一点，即nums[k+] <= nums[k-]。通过上一题，我们可以知道，二分查找可以通过缩小搜索区间，找出这种使关系发生变化的点。

旋转点左侧为第一分枝，右侧为第二分枝。我们的目标就是，通过缩小收缩区间，找到第二分枝的左端点，即为旋转点。如果中点m在第二分枝上，根据单调性，有r > m && nums[r] >= nums[m]，那么收缩r=m，使得r保持在第二分枝上。如果r=m-1的话，无法保证还在第二分枝，因为我们只验证过r和m的单调性，没有验证r和m-1的单调性。如果中点m在第一分枝上，则恰好r在旋转点（即第二分枝左端点）右侧，m在旋转点左侧，有nums[r] < nums[m]，那么抛弃中点m及其左边的点，l=m+1。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int findMin(int[] nums) {
        int l = 0, h = nums.length - 1;
        while (l < h) {
            int m = l + (h - l) / 2;
            if (nums[m] <= nums[h]) {
                h = m;
            } else {
                l = m + 1;
            }
        }
        return nums[l];
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def findMin(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if nums[m] == nums[r]:
                break
            elif nums[r] < nums[m]:
                l = m + 1
            else:
                r = m 
        return nums[l]

总结

上面两道题使用二分查找解题的关键都在于，能够将要找的target与某种关系联系起来。在target的左侧，满足某种关系；在target的右侧，不满足这种关系。

第十题

154. 寻找旋转排序数组中的最小值 II

代码

python版本

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def findMin(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if nums[r] == nums[m]:
                r -= 1
            elif nums[r] > nums[m]:
                r = m
            else:
                l = m + 1
        return nums[l]

第十一题

240. 搜索二维矩阵 II

题目描述：
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例1：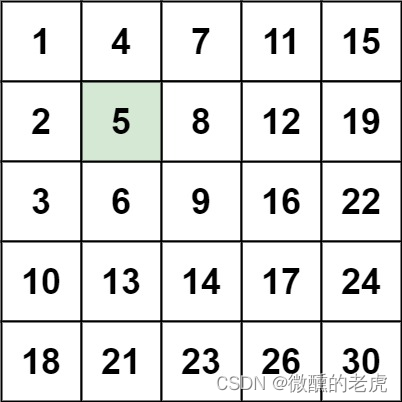
在这里插入图片描述

1
2
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

思路

在上面两道题中我已经谈到了，可以使用二分查找将target与某种关系联系起来，在target的左侧满足某种关系，而在target的右侧不满足这种关系。在这道题中，这种关系是结构上的。对于任意一个元素，其所在行自左向右递增，所在列自上而下递增。特别的，对于每一行最右的元素m，其左的所在行元素都比它小，其下的所在列元素都比它大。因此，如果给定一个target和m进行比较，target小于m则应该向其左的所在行元素继续比较；target大于m则应该向其下的所在列元素继续比较。如果m的位置超出矩阵的合法范围，则说明找不到target。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int i = 0, j = n - 1;
        while(i < m && j >= 0){
            if(target == matrix[i][j]){
                return true;
            }
            else if(target < matrix[i][j]){
                j--;
                continue;
            }
            else{
                i++;
            }
        }
        return false;     
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m = len(matrix)
        n = len(matrix[0])
        x, y = 0, n - 1
        while x < m and y >= 0:
            if matrix[x][y] == target:
                return True
            elif matrix[x][y] < target:
                x += 1
            else:
                y -= 1
                
        return False

总结

这一题和前面两题一样，都需要寻找一种关系作为突破口。在某个点之前，这种关系存在；在某个点之后，这种关系不存在。

第十二题

378. 有序矩阵中第 K 小的元素

题目描述：
给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是 排序后 的第 k 小元素，而不是第 k 个 不同 的元素。

你必须找到一个内存复杂度优于 O(n2) 的解决方案。

示例1：

1
2
3
输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13

思路

我们先分析这道题为什么可以用二分查找来解决。正如前面三题所示，能够用二分查找解决的问题都存在一种关系，在target之前满足这种关系，在target之后不满足这种关系。让我们来看示例1，在数组[1,5,9,10,11,12,13,13,15]中，如果一个元素是target，那么数组中比它小的元素有8个；如果一个元素小于target，那么数组中比它小的元素小于8个；如果一个元素大于target，那么数组中比它小的元素大于8个。这种关系的存在，使得我们可以用二分查找来解决这道题。在这里，给出一个二分查找的思路作为参考，二分，超级简单。

关于这个思路，很多人会纠结的一点是，如何验证最后求得的l在数组中？其实就是在问，如果一个元素是target，那么数组中比它小的元素有8个；反过来，如果数组中比一个数小的元素有8个，那么这个元素到底是不是target？不难发现，“一个元素是target，那么数组中比它小的元素有8个”是个充分不必要条件。不妨把数组[1,5,9,10,11,12,13,13,15]最后的15改成30来讨论这个问题。对于数组[1,5,9,10,11,12,13,13,30]，我们还是寻找第8小的元素，正确答案应该是13。但是，在13和30中间，其实还有很多个数满足“数组中比一个数小的元素有8个”这个条件。准确来说，14，15，…，29都满足这个条件。我称这些数为“影子target”。很多人就会纠结，按照二分，超级简单的思路，那么如何排除掉这些“影子target”？这里我们就得先想明白，为什么会存在“影子target”。简单来说，“影子target”就是target和target后一位之间的间隙。如果我们把最后一位改成20，那么正确答案还是13，“影子target”是14，15，…，19。如果我们把数组改成[1,5,9,10,11,12,13,16,20]，那么正确答案是16，“影子target”是17，18，19。那么，我们会发现，16是满足“数组中比一个数小的元素有8个”这个条件的最小的数。

让我们从头思考一下这个问题。为什么我们可以用二分查找来解决这道问题？因为在数组中，如果一个元素是target，那么数组中比它小的元素个数cnt等于8；如果一个元素小于target，那么数组中比它小的元素个数cnt小于8；如果一个元素大于target，那么数组中比它小的元素cnt大于8。所以，我们可以用二分查找解决这道题。cnt小于8，则l=m+1；cnt大于8，则r=m-1。但是，cnt等于8时，我们就找到target了吗？上面已经分析过了，如果cnt等于8，那么这个元素不一定是target，还有可能是“影子target”。因为在target和target后一位之间，还有间隙。那么我们如何找到正确的target呢？我们已经发现，真实target就是满足cnt等于8的最小值，所以我们就是在找满足cnt等于8这个条件的左边界。既然是找左边界，在上一篇博客中我已经讨论过了，其实就是在找到满足cnt等于8这个条件的元素时，不要直接返回结果，而是继续收缩右边界。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        int n = matrix.length, l = matrix[0][0], r = matrix[n - 1][n - 1], cnt = 0;
        while(l <= r){
            int m = l + (r - l) / 2;
            cnt = 0;
            for(int i = 0; i < n; i++){
                for(int j = 0; j < n && matrix[i][j] <= m; j++){
                    cnt++;
                }
            }
            if(cnt < k){
                l = m + 1;
            }
            else{
                r = m - 1;
            }
        }
        return l;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        n = len(matrix)
        l = matrix[0][0]
        r = matrix[n - 1][n - 1]
        while l <= r:
            m = l + (r - l) // 2
            count = 0
            for row in matrix:
                for col in row:
                    if col <= m:
                        count += 1
            
            if k > count:
                l = m + 1
            else:
                r = m - 1

        return l

总结

这道题不难想到用二分查找来解决。一般人或许可以想到用官方题解差不多的二分法。但是，上面介绍的二分法，需要对为什么可以用二分法，用二分法是查找target还是左/右边界有深刻的理解。

参考：
Leetcode 题解 - 二分查找
二分，超级简单

发表于
本文字数： 6.2k 阅读时长 ≈ 11 分钟

@TOC

接上文LeetCode算法题解——二分查找1，本篇总结LeetCode中部分题目的二分查找解法。

第四题（寻找左边界）

278. 第一个错误的版本

题目描述：
你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例1：

1
2
3
4
5
6
7
输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false 
调用 isBadVersion(5) -> true 
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。

思路

如果将n个版本的true和false放到一个数组里，应该是[false, false, …, true, true]，前面都是false，后面都是true。这道题可以看作是找到最后一个false，也可以看作是找到第一个true。在这里，我将它当作找到第一个true来做，也就是寻找true的左边界。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        // 左闭右闭
        int l = 1;
        int r = n;
        // 寻找true的左边界
        while(l <= r){
            // 防止溢出
            int m = l + (r - l) / 2;
            // 能找到，缩小右边界
            if(isBadVersion(m) == true){
                r = m - 1;
            }
            // 找不到，缩小左边界
            else if(isBadVersion(m) == false){
                l = m + 1;
            }
        }
        return l;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
class Solution:
    def firstBadVersion(self, n: int) -> int:
        l, r = 1, n
        while l <= r:
            m = l + (r - l) // 2
            if isBadVersion(m):
                r = m - 1
            else:
                l = m + 1
        return l

总结

在寻找左边界的时候，和之前中点值找到target一样，找到就收缩右边界。拓展一下，在寻找左/右边界，找到了target，但还没有到达其边界，应该向你要搜索的边界靠近，进一步压缩搜索空间。

第五题（寻找右边界）

744. 寻找比目标字母大的最小字母

题目描述：
给你一个字符数组 letters，该数组按非递减顺序排序，以及一个字符 target。letters 里至少有两个不同的字符。

返回 letters 中大于 target 的最小的字符。如果不存在这样的字符，则返回 letters 的第一个字符。

示例1：

1
2
3
输入: letters = ["c", "f", "j"]，target = "a"
输出: "c"
解释：letters 中字典上比 'a' 大的最小字符是 'c'。

思路

按照题意，寻找第一个比target大的字母。在前面寻找右边界时我们已经提到，当循环停止时右边界r以右的元素都大于target，则右边界r以左的元素都小于等于target，右边界r即最后一个target。所以，第一个比target大的字母就是r+1处的字母。但是当target比数组中所有数字都要大的时候，r+1会越界，这里需要做特别处理。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public char nextGreatestLetter(char[] letters, char target) {
        // 左闭右闭
        int l = 0;
        int r = letters.length - 1;
        // 寻找右边界
        while(l <= r){
            // 防止溢出
            int m = l + (r - l) / 2 ;
            // 收缩左边界
            if(target >= letters[m]){
                l = m + 1;
            }
            // 收缩右边界
            else{
                r = m - 1;
            }
        }
        // 防止越界，当不存在这样的字符，即target最大
        if(r == letters.length - 1){
            return letters[0];
        }
        return letters[r + 1];
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
class Solution:
    def nextGreatestLetter(self, letters: List[str], target: str) -> str:
        l, r = 0, len(letters) - 1
        while l <= r:
            m = l + (r - l) // 2
            if target >= letters[m]:
                l = m + 1
            else:
                r = m - 1
        return letters[(r + 1) % len(letters)]

总结

这道题，需要将大于 target 的最小的字符理解成第一个比target大的字符，并且知道可以通过寻找target的右边界来求解。

第六题（找一个数）

367. 有效的完全平方数

题目描述：
给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。

不能使用任何内置的库函数，如 sqrt 。

示例1：

1
2
3
输入：num = 16
输出：true
解释：返回 true ，因为 4 * 4 = 16 且 4 是一个整数。

思路

首先思考一种暴力算法。以num=16为例，我们先从1开始穷举。1*1=1，1<16，不满足。2*2=4，4<16，不满足。3*3=9，9<16，不满足。4*4=16，16==16，满足！5*5=25，25>16，不满足。显然，比4小的数和比4大的数，都不满足，我们可以通过二分法筛选掉比4小的数和比4大的数。

值得注意的是，如果直接比较x*x和num，可能x*x会超过int的范围。可以转化为比较x和num/x。如果是这样的话，考虑到整数除法结果仍然为整数，当x=num/x时，num可能是x*x，x*x+1，…，x*x+(x-1)。此时只需要再次比较x*x和num，即可。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean isPerfectSquare(int num) {
        // 左闭右闭
        int l = 1;
        int r = num;
        while(l <= r){
            // 防止溢出
            int m = l + (r - l) / 2;
            int sqrt = num / m;
            // 找到target并进行判断
            if((m == sqrt) && (m * sqrt == num)){
                return true;
            }
            else if(m < sqrt){
                l = m + 1;
            }
            else{
                r = m - 1;
            }
        }
        return false;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def isPerfectSquare(self, num: int) -> bool:        
        l, r = 1, num
        while l <= r:
            m = l + (r - l) // 2
            sqrt = num // m
            if sqrt < m:
                r = m - 1
            else:
                l = m + 1
        
        return r * r == num

总结

这道题，我们可以先思考一个穷举的办法，然后考虑可以用二分法进行优化。防止溢出是一个需要注意的点。这道题里，m是中点，sqrt是target。和以前不同，这道题的target是会变的。

第七题（找右边界）

69. x 的平方根

题目描述：
给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例1：

1
2
3
输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

思路

这题和上一题不同。在上一题中，完全平方数，如16，一定能找到整数4*4=16。但是在这题里，将平方根的小数部分舍去了，那么就不能通过x*x=num来进行判断。同样的，我们先思考一种暴力算法。以num=8为例，我们先从1开始穷举。1*1=1，1<8；2*2=4，4<8；3*3=9，9>8。显然，前面的平方数都比8小，后面的平方数都比8大，我们需要找到最后一个比8小的平方数。问题转化为了找比8小的平方数的右边界。

和上一题一样，如果直接比较x*x和num，可能x*x会超过int的范围，可以转化为比较x和num/x。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int mySqrt(int x) {
        if(x <= 1){
            return x;
        }
        // 左闭右闭
        int l = 1;
        int r = x;
        while(l <= r){
            // 防止溢出
            int m = l + (r - l) / 2;
            int sqrt = x / m;
            if(m > sqrt){
                r = m - 1;
            }
            else{
                l = m + 1;
            }
        }
        return r;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 0:
            return x

        l, r = 1, x
        while l <= r:
            m = l + (r - l) // 2
            sqrt = x // m
            if sqrt < m:
                r = m - 1
            else:
                l = m + 1
        return r

总结

同样的，这道题我们先思考一个穷举的办法，然后考虑可以用二分法进行优化。防止溢出依旧是一个需要注意的点。这道题里，m是中点，sqrt是target，会发生改变。

下一篇博客LeetCode算法题解——二分查找3中，我将分享LeetCode中几道比较难想到使用二分查找解法的题目。

参考:

二分查找算法细节详解，顺便写了首诗

发表于
本文字数： 6.6k 阅读时长 ≈ 12 分钟

@TOC
常用的二分查找包括：寻找一个数、插入target、寻找左右边界。

第一题（寻找一个数）

704. 二分查找

题目描述：
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例1：

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

思路

二分法，如果找到target，直接返回；如果target比中点值小，说明在左区间，则缩小右端点；如果target比中点值大，说明在右区间，则缩小左端点。

代码

c++版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int binarySearch(vector<int> nums, int target) 
{
	// 查找区间
    int l = 0; 
    int r = nums.size() - 1;
    // 终止条件
    while(l <= r) 
    {
    	// 中点计算
        int m = l + (r - l) / 2;
        // 区间缩减
        if(nums[m] == target)
            return m; 
        else if (nums[m] < target)
            l = m + 1;
        else if (nums[m] > target)
            r = m - 1;
    }
    return -1;
}

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int search(int[] nums, int target) {
        // 左闭右闭
        int l = 0;
        int r = nums.length - 1;
        while(l <= r){
            // 防止溢出
            int m = l + (r - l) / 2;
            if(target == nums[m]){
                // 如果找到，直接返回
                return m;
            }
            else if(target > nums[m]){
                // 右边界缩小
                r = m - 1;
            }
            else if(target > nums[m]){
                // 左边界缩小
                l = m + 1;
            }
        }
        // 未找到，返回-1
        return -1;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if target == nums[m]:
                return m
            elif target < nums[m]:
                r = m - 1
            else:
                l = m + 1
        return -1

总结

本题有两点需要注意。
第一点，搜索区间是“左闭右闭”。之所以选择“左闭右闭”的搜索区间，是为了在缩小左、右端点的时候可以统一操作。此外，因为搜索区间是“左闭右闭”的，所以循环条件是左端点小于等于右端点。
第二点，取中点的计算要防溢出。

第二题（插入target）

35. 搜索插入位置

题目描述：
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例1：

1
2
输入: nums = [1,3,5,6], target = 2
输出: 1

思路

如果找得到，则参考上题代码。如果找不到，循环停止时，左边界l以左（不包含l）的元素都小于target，右边界r以右（不包含r）的元素都大于target。所以，target应该插入左边界l的位置，这样其左侧元素皆小于target，其右侧元素皆大于target。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int searchInsert(int[] nums, int target) {
        // 左闭右闭
        int l = 0;
        int r = nums.length - 1;
        while(l <= r){
            // 防止溢出
            int m = l + (r - l)/2;
            if(target == nums[m]){
                // 如果找到，直接返回
                return m;
            }
            else if(target > nums[m]){
                // 右边界缩小
                r = m - 1;
            }
            else if(target > nums[m]){
                // 左边界缩小
                l = m + 1;
            }
        }
        // 返回左边界
        return l;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if nums[m] == target:
                return m
            elif target < nums[m]:
                r = m - 1
            else:
                l = m + 1
        return l

总结

循环停止时，左边界l以左（不包含l）的元素都小于target，右边界r以右（不包含r）的元素都大于target。所以，target应该插入左边界l的位置，这样其左侧元素皆小于target，其右侧元素皆大于target。

第三题（寻找左右边界）

34. 在排序数组中查找元素的第一个和最后一个位置

题目描述：
给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例1：

1
2
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

思路

先考虑左边界。和前面两题不同，这题找到target不能直接返回，要继续寻找，直到找到第一个target。当循环停止时，左边界l以左的元素都小于target，则左边界l以右的元素都大于等于target，左边界l即第一个target。所以，当找到target的时候，仍然缩小右边界，向左边界靠拢。

同理，搜索右边界时，当找到target不能直接返回，要继续寻找，直到找到最后一个target。当循环停止时，右边界r以右的元素都大于target，则右边界r以左的元素都小于等于target，右边界r即最后一个target。所以，当找到target的时候，仍然缩小左边界，向右边界靠拢。

得到了左右边界，也只是说明如果有target，那第一个和最后一个target就是左右边界。但是，存在没有target的可能，所以还需要对左右边界进行判断。值得注意的是，可能target比所有的元素都大，此时左边界l等于数组长度，需要先判断是否越界，再判断左边界是否为target。同样的，可能target比所有的元素都小，此时右边界l等于-1，需要先判断是否越界，再判断右边界是否为target。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int results[] = new int[]{-1, -1};
        // 左闭右闭
        int l = 0;
        int r = nums.length - 1;
        // 寻找第一个target
        while(l <= r){
            // 防止溢出
            int m = l + (r - l) / 2;
            // 缩小右边界
            if(target <= nums[m]){
                r = m - 1;
            }
            // 缩小左边界
            else if(target > nums[m]){
                l = m + 1;
            }
        }
        // 防止越界
        if((l < nums.length) && (nums[l] == target)){
            results[0] = l;
        }
        // 左闭右闭
        l = 0;
        r = nums.length - 1;
        // 寻找最后一个target
        while(l <= r){
             // 防止溢出
            int m = l + (r - l) / 2;
            // 缩小左边界
            if(target >= nums[m]){
                l = m + 1;
            }
            // 缩小右边界
            else if(target < nums[m]){
                r = m - 1;
            }
        }
        // 防止越界
        if((r >= 0) && (nums[r] == target)){
            results[1] = r;
        }
        return results;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        if nums == None or len(nums) == 0:
            return [-1, -1]
        
        result = [-1, -1]

        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if target <= nums[m]:
                r = m - 1
            else:
                l = m + 1
        
        if l < len(nums) and nums[l] == target:
            result[0] = l
        
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if target >= nums[m]:
                l = m + 1
            else:
                r = m - 1
        
        if r >= 0 and nums[r] == target:
            result[1] = r

        return result

总结

本题有三点需要注意。

第一点，理解为什么左右边界就是第一个和最后一个target。当循环停止时，左边界l以左的元素都小于target，则左边界l以右的元素都大于等于target，左边界l即第一个target。当循环停止时，右边界r以右的元素都大于target，则右边界r以左的元素都小于等于target，右边界r即最后一个target。

第二点，当找到target的时候左右边界如何移动。寻找左边界时，需要右边界向左边界靠拢，所以找到target时仍然缩小右边界。寻找右边界时，需要左边界向右边界靠拢，所以找到target时仍然缩小左边界。

第三点，防止左右边界越界。左右边界是target“应该”出现的第一个和最后一个位置，到底是不是还需要经过验证。验证之前，记得考虑左右边界是否越界。

下一篇博客LeetCode算法题解——二分查找2，我将总结LeetCode中部分题目的二分查找解法。

参考:

二分查找算法细节详解，顺便写了首诗

发表于
本文字数： 6k 阅读时长 ≈ 11 分钟

@TOC

这里介绍双指针在数组中的第一类题型：一个数组当两个用。

第一题

88. 合并两个有序数组

题目描述：
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例1：

1
2
3
4
输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

思路

一个简单的想法，借助新建数组nums3来完成nums1和nums2的合并。如果nums1[0]小于nums2[0]，则将nums1[0]放入nums3[0]，继续比较nums1[1]和nums2[0]。同样的，如果nums2[0]小于nums1[0]，则将nums2[0]放入nums3[0]，继续比较nums2[1]和nums1[0]。直到将nums1或nums2遍历完，剩下未遍历的部分可以直接放入nums3。

但是，题目要返回的是nums1而不是nums3。那么我们有两个办法来对上述的方法进行优化。第一个办法，最后遍历nums3，用nums3的元素替换nums1的元素。第二个办法，直接在nums1上进行上述的操作。如果要在nums1上进行上述的操作，那么就需要从大到小比较，先把最大的元素放到nums1最右侧，以免覆盖了未参与比较的nums1元素。

直接把nums1数组当nums3数组来用，就是双指针的精髓所在。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int idx1 = m-1, idx2 = n - 1, idx = m + n - 1;
        while(idx1>=0 || idx2 >=0){
            if(idx1 < 0){
                nums1[idx--] = nums2[idx2--];
            }
            else if(idx2 < 0){
                nums1[idx--] = nums1[idx1--];
            }
            else if(nums1[idx1] > nums2[idx2]){
                nums1[idx--] = nums1[idx1--];
            }
            else{
               nums1[idx--] = nums2[idx2--]; 
            }
        }
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        idx1, idx2, idx3 = m - 1, n - 1, m + n - 1
        while idx1 >= 0 and idx2 >= 0:
            if nums1[idx1] > nums2[idx2]:
                nums1[idx3] = nums1[idx1]
                idx3 -= 1
                idx1 -= 1
            else:
                nums1[idx3] = nums2[idx2]
                idx3 -= 1
                idx2 -= 1
        
        while idx3 >= 0 and idx2 >= 0:
                nums1[idx3] = nums2[idx2]
                idx3 -= 1
                idx2 -= 1

第二题

27. 移除元素

题目描述：
给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例1：

1
2
3
输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

思路

如果不要求原地修改，那很简单。只需要新建数组nums1，从左到右扫描nums的元素，如果nums的元素不等于val，则将其放入nums1；如果等于val，则跳过。

但是，现在要求原地修改，也就是要一个数组当作两个用。和上一题一样，有两种办法。第一种办法，可以先把元素放在数组nums1，然后再用nums1的元素去覆盖nums的元素。第二种办法，可以直接把nums数组当nums1数组。但是，这样会不会导致nums原有的元素被覆盖呢？实际上是不会的，我们思考一下，如果用idx1扫描nums，非val元素通过idx2存放到nums1，那么idx1总是大于等于idx2的。也就是说，idx2使用的区域，idx1早就扫描过了。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int removeElement(int[] nums, int val) {
        int slow = 0;
        int fast = 0;
        for(; fast < nums.length; fast++){
            if(nums[fast] != val){
                nums[slow] = nums[fast];
                slow++;
            }
        }
        return slow;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        n = len(nums)
        slow, fast = 0, 0
        while fast < n:
            if nums[fast] != val:
                nums[slow] = nums[fast]
                slow += 1
            fast += 1
        return slow

第三题

283. 移动零

题目描述：
给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例1：

1
2
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

思路

这题和上一题很相似，都是遇到val（0）就跳过。但是不同的是，这道题不仅要跳过val，还要把val放到后面去。有两种办法，第一种是和第二题一样，遇到val的时候就跳过val，然后再把后面都填充为val；第二种是让val和非val进行交换。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public void moveZeroes(int[] nums) {
        int slow = 0;
        int fast = 0;
        final int val = 0;
        for(; fast < nums.length; fast++){
            if(nums[fast] != val){
                int temp = nums[slow];
                nums[slow] = nums[fast];
                nums[fast] = temp;
                slow++;
            }
        }
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        n = len(nums)
        slow, fast = 0, 0
        while fast < n:
            if nums[fast] != 0:
                nums[slow], nums[fast] = nums[fast], nums[slow]
                slow += 1
            fast += 1

第四题

26. 删除有序数组中的重复项

题目描述：
给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

示例1：

1
2
3
输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

思路

如果不是原地修改，那我们还是考虑新建数组nums1。nums[0]肯定是不重复的，可以放到nums1[0]。因为nums是有序的，从nums[1]开始，如果和前面的元素相同，那么说明是重复的，可以跳过；如果和前面的元素不同，那么说明不重复，放入nums1数组。

如果要原地修改，还是同样的情况，有两种办法。第一种办法就是用nums1去覆盖nums。第二种办法，要一个数组当作两个用。我们总是要思考，会不会覆盖未扫描的元素？看得出，fast总是比slow跑得快，所以不会覆盖。

代码

java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int removeDuplicates(int[] nums) {
        int slow = 0;
        int fast = 0;
        for(; fast < nums.length; fast++){
            if(nums[fast] != nums[slow]){
                slow += 1;
                nums[slow] = nums[fast];
            }
        }

        return slow + 1;
    }
}

python版本

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        n = len(nums)
        slow, fast = 0, 0
        while fast < n:
            if nums[fast] != nums[slow]:
                slow += 1
                nums[slow] = nums[fast]

            fast += 1
        
        return slow + 1

下一篇博客LeetCode算法题解——双指针2中，我将分享LeetCode中另一种类型的双指针问题。

参考：

Leetcode 题解 - 双指针